class: bottom, right, inverse <!--- Para correr en ATOM - open terminal, abrir R (simplemente, R y enter) - rmarkdown::render('static/docpres/02_bases/2mlmbases.Rmd', 'xaringan::moon_reader') About macros.js: permite escalar las imágenes como [scale 50%](path to image), hay si que grabar ese archivo js en el directorio. ---> .pull-left[.center[ <br> <br> <br> <br> <br> <br> <br> <br> ]] .pull-right[ # Modelos Multinivel ### Juan Carlos Castillo ### Sociología FACSO - UChile ### 2do Sem 2019 ### [multinivel.netlify.com](https://multinivel.netlify.com) <br> ## Sesión 2: Bases ] --- # Introducción ### Resumen sesión anterior - Concepto curso - Investigación aplicada - Orientación práctica - Introductorio - Acomodación esquema de regresión simple a problemas con más de 1 nivel -- - Contexto y relaciones micro-macro en sociología -- - Problema de falacia ecológica --- ## Idea de falacia ecológica .center[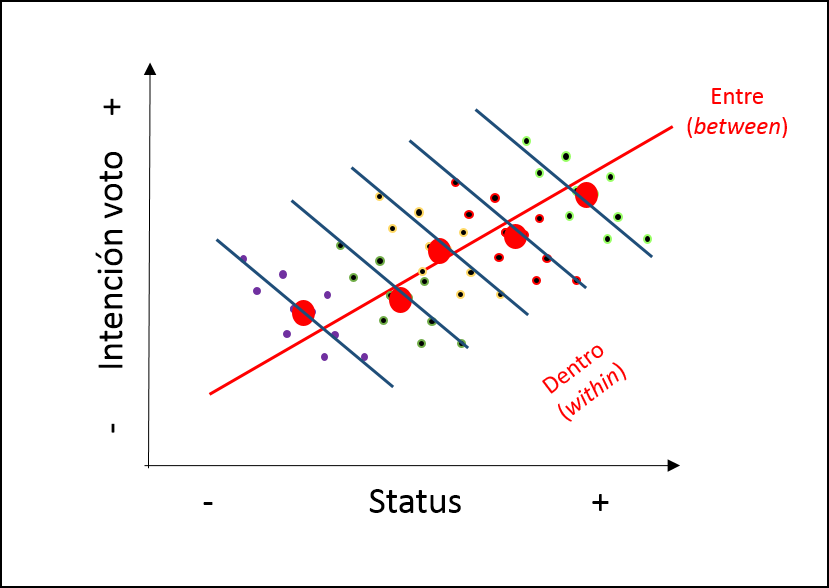] --- ## Contexto e implicancias teóricas En el planteamiento de una investigación con hipótesis multinivel, es relevante definir: ### - Qué es el **contexto** en nuestra investigación ### - Cuáles son los elementos principales del contexto a considerar en las hipótesis ### - Cómo se relacionan variables del contexto con variables individuales (hipótesis multinivel) --- ## Formas de estimación multinivel Modelo multinivel con predictores individuales y contextuales 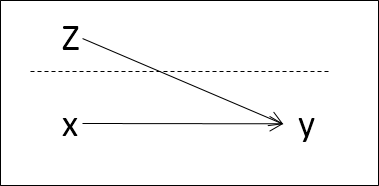 --- ## Formas de estimación multinivel Modelo multinivel con interacción entre niveles 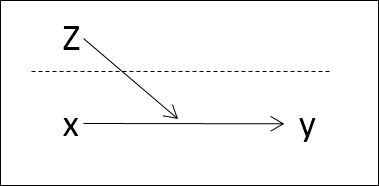 --- ## Contexto e implicancias estadísticas - Los modelos multinivel tienen dos sentidos principales a nivel estadístico: - Corregir estimaciones con variables individuales cuando existe dependencia contextual (estimación más adecuada del error) - Hace posible contrastar hipótesis que abarcan relaciones entre niveles --- class: inverse, right, middle # **ESTA CLASE** <br> # Regresión y residuos # Residuos y dependencia contextual # Idea de efecto aleatorio --- class: roja, middle, center # Regresión y residuos --- ## Bases: Modelo de regresión Objetivos centrales de la regresión: -- 1. Conocer la variación de una variable (dependiente, Y) de acuerdo a la variación de otra variable (independiente, X): - Ej: En qué medida el puntaje PSU influye en el éxito académico en la universidad? ... -- 2. Estimar el valor de una variable de acuerdo al valor de otra (predicción) - Ej: Si una persona obtiene 600 puntos en la PSU, que promedio de notas en la universidad es probable que obtenga? (Atención: predicción no implica explicación) -- 3. Establecer en que medida esta asociación es significativa (inferencia) --- ## Bases - varianza `$$\begin{aligned} \sigma^2 = \frac{\sum_{i=1}^{n}(x_i - \bar{x})^2} {n-1}=\frac{\sum_{i=1}^{n}(x_i - \bar{x})(x_i - \bar{x})} {n-1} \end{aligned}$$` - covarianza `$$\begin{aligned} cov(x,y) = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})} {n-1} \end{aligned}$$` - correlación `$$\begin{aligned} r= \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})} {(n-1)\sigma_x \sigma_y } \end{aligned}$$` --- ## Bases .pull-left[ - La (co) variación general de Y respecto a X se puede expresar en una ecuación de la recta = modelo de regresión - Para estimar la “mejor recta” se utiliza la *recta de mínimos cuadrados* (OLS – Ordinary Least Squares) - OLS es un estimador que minimiza la suma de los cuadrados de las distancias entre las observaciones y la recta en el eje vertical ] .pull-right[ 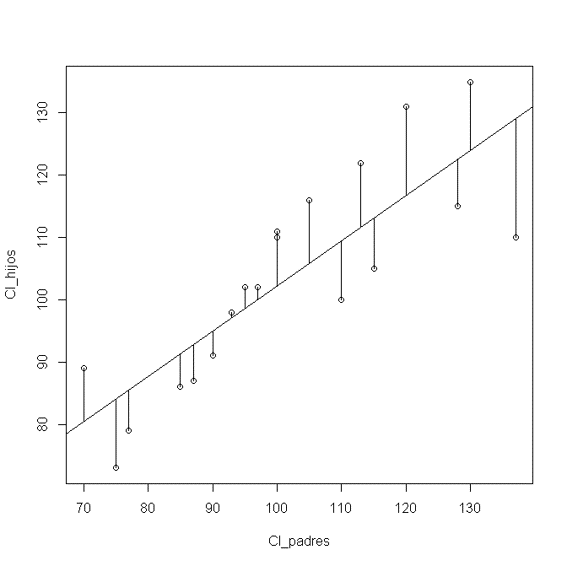 ] --- ## Bases Donde ... `$$\begin{aligned} Y=a+bX+e\end{aligned}$$` - a= intercepto, el valor de Y cuando X es 0 - b= pendiente (coeficiente de regresión), es el valor que me permite estimar el puntaje de Y mediante el puntaje de X - e= residuo, da cuenta de las fuentes de variabilidad distintas de X en la predicción de Y. O sea, es la parte de Y que no es explicada por X. --- # Bases Estimación de los coeficientes de la ecuación: `$$\begin{aligned} b=\frac{\Sigma xy}{\Sigma x^2}&=\frac{\Sigma((x-\bar{x})(y-\bar{y}))}{\Sigma (x-\bar{x})} \\ a&=\bar{Y}-b \bar{X} \\ {Y}^{\prime }&=a+bX \end{aligned}$$` -- - La ecuación de regresión permite predecir valores de Y para cada valor de X --- # Bases - Tres piezas de información relevante: -- - Valor observado de Y -- - Estimación de Y a partir de X =( `\({Y}^{\prime }\)` ) -- - Promedio de Y ( `\(\bar{Y}\)` ) .center[] --- # Bases `$$\begin{aligned} Y&=\bar{Y}+({Y}^{\prime}-\bar{Y})+(Y-{Y}^{\prime})\\ Y-\bar{Y}&=({Y}^{\prime}-\bar{Y}) + (Y-{Y}^{\prime}) \\ \Sigma(y_i - \bar{y})^2 &=\Sigma (\bar{y}-\hat{y}_i)^2 + \Sigma(y_i-\hat{y}_i)^2 \\ SS_{tot}&=SS_{reg}+SS_{error} \end{aligned}$$` --  --- # Bases Por lo tanto: `$$SS_{tot}=SS_{reg}+SS_{error}$$` `$$\frac{SS_{tot}}{SS_{tot}}=\frac{SS_{reg}}{SS_{tot}}+\frac{SS_{error}}{SS_{tot}}$$` `$$1= \frac{SS_{reg}}{SS_{tot}} + \frac{SS_{error}}{SS_{tot}} \\ \frac{SS_{reg}}{SS_{tot}}= ?$$` -- `$$R^2$$` --- class: roja, middle, center # Dependencia contextual --- ## Residuos y dependencia contextual  --- ## Residuos y dependencia contextual  --- ## Residuos y dependencia contextual  --- ## Residuos y dependencia contextual  --- # Implicancias para el modelo de regresión: - Dependencia de los residuos - Pérdida de información, mayor error - Alternativas? Descomposición de la varianza de los residuos *entre* y *dentro* los grupos= en distintos niveles = **multinivel**. - En concreto, se agrega un término de error adicional al modelo: `\(\mu_{0j}\)` - Este término de error se expresa como un **efecto aleatorio** (como opuesto a *efecto fijo*) --- class: roja, middle, center # Modelo y parámetros --- ## Modelo con coeficientes aleatorios (RCM) - Random Coefficients Models (RCM) o Mixed (effects) Models - Forma de estimación de modelos multinivel - Idea base: se agrega un parámetro *aleatorio* al modelo, es decir, que posee variación en relación a unidades de nivel 2. --- ## Parámetros  --- ## Parámetros Detalles de la notación : - `\(_i\)` es el índice asociado a los individuos - `\(_j\)` es el índice asociado a la pertenencia a grupos ($_j=1 ..., N$) - `\(y_{ij}\)` es la variable dependiente - `\(X_{i}\)` es la variable independiente de nivel individual - `\(\beta\)` y `\(\gamma\)` son coeficientes de regresión - `\(Z_j\)` es la variable independiente a nivel grupal - `\(r_{ij}\)` es el residuo a nivel individual - `\(\mu_{j}\)` es un residuo/desviación de nivel grupal - `\(\tau_{00}\)` es la varianza de `\(\mu_{0j}\)` - `\(\sigma^2\)` es la varianza de `\(r_{ij}\)` --- class: inverse, right # Resumen .pull-left[.left[ <br> <br> <br> <br> <br> <br> <br>  ]] .pull-right[ ## - Regresión y residuos ## - Residuos y dependencia contextual ## - Parametrizando la dependencia contextual a través de un efecto aleatorio ] --- class: roja, middle, center # Práctica --- ## High School & Beyond (HSB) data - High School & Beyond (HSB) es una muestra representativa nacional de educación secundaria publica y católica de USA implementada por el National Center for Education Statistics (NCES). - Más información en [https://nces.ed.gov/surveys/hsb/](http://nces.ed.gov/surveys/hsb) - Level 1 variables: - minority, etnicidad (1 = minority, 0 =other) - female, student gender (1 = female, 0 = male) - ses, (medida estandarizada de nivel socioeconómico en base a variables como educación de los padres, ocupación e ingreso) - mathach, logro en matemática --- ## High School & Beyond (HSB) data - Level 2 variables: - size (matricula) - sector (1 = Catholic, 0 = public) - pracad (proportion of students in the academic track) - disclim (a scale measuring disciplinary climate) - himnty (1 = more than 40% minority enrollment, 0 = less than 40%) - meanses (mean of the SES values for the students in this school who are included in the level-1 file) - Cluster variable= id (school id)