Modelos Multinivel

class: bottom, right, inverse

<!---
Para correr en ATOM
- open terminal, abrir R (simplemente, R y enter)
- rmarkdown::render('static/docpres/02_bases/2mlmbases.Rmd', 'xaringan::moon_reader')

About macros.js: permite escalar las imágenes como [scale 50%](path to image), hay si que grabar ese archivo js en el directorio.
--->

.pull-left[.center[
 
 
 
 
 
 
 
 
![:scale 70%](https://multinivel.netlify.com/images/hex_eic2.png)]]

.pull-right[
# Modelos Multinivel
### Juan Carlos Castillo
### Sociología FACSO - UChile
### 2do Sem 2019
### [multinivel.netlify.com](https://multinivel.netlify.com)

## Sesión 3: Regresión con datos individuales y agregados
]

---
class: roja, middle, center

# Resumen sesión anterior

---
## Residuos y dependencia contextual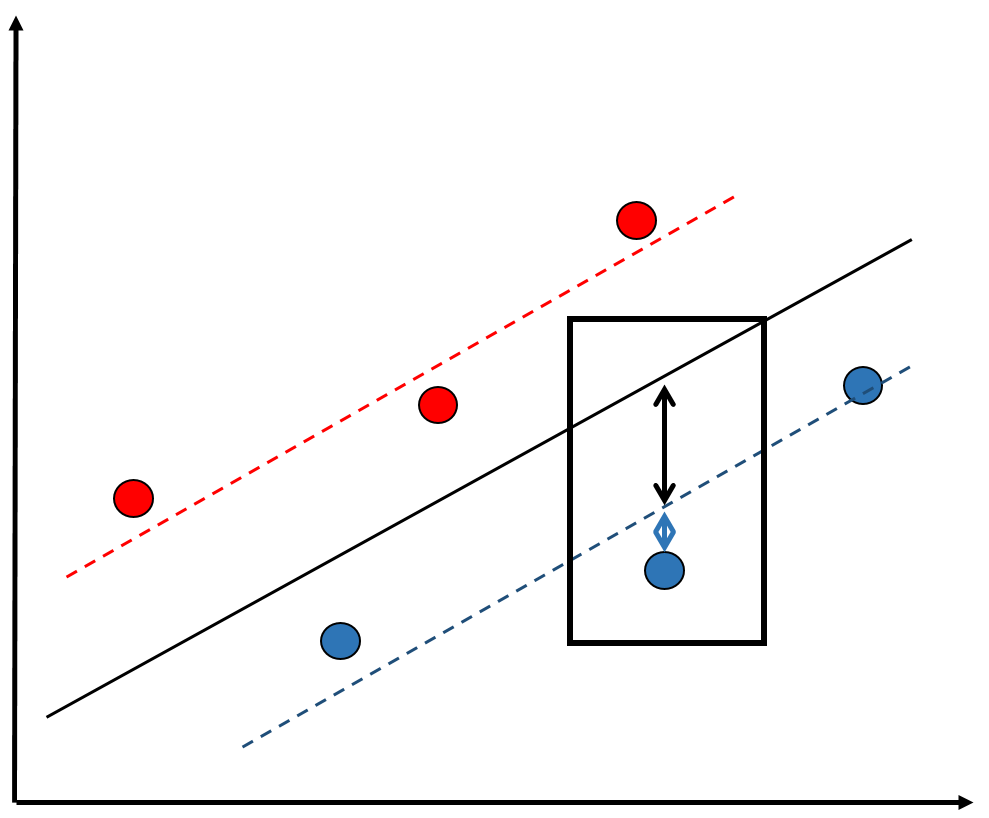

![:scale 70%](images/res_mul4.png)

---
# Implicancias para el modelo de regresión:

-   Dependencia de los residuos

-   Pérdida de información, mayor error

-   Alternativas? Descomposición de la varianza de los residuos *entre* y
*dentro* los grupos= en distintos niveles = **multinivel**.

-   En concreto, se agrega un término de error adicional al modelo:
`$\mu_{0j}$`

-   Este término de error se expresa como un **efecto aleatorio** (como opuesto a *efecto fijo*)

---
## Parámetros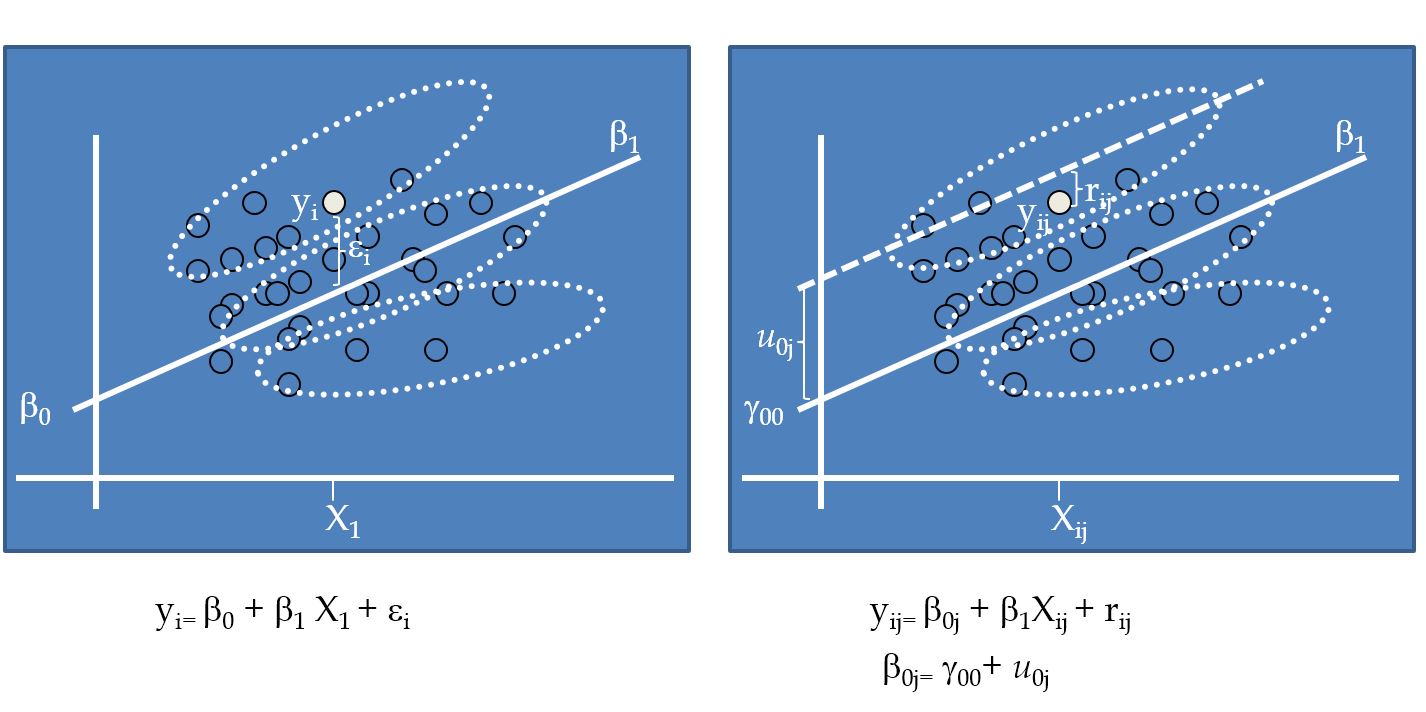

![](images/paramet.JPG)

---
## Práctica: High School & Beyond (HSB) data

-   High School & Beyond (HSB) es una muestra representativa nacional de educación secundaria publica y católica de USA implementada por el National Center for Education Statistics (NCES).

-   Más información en [https://nces.ed.gov/surveys/hsb/](http://nces.ed.gov/surveys/hsb)

-   Level 1 variables:

-   minority, etnicidad (1 = minority, 0 =other)

-   female, student gender (1 = female, 0 = male)

-   ses, (medida estandarizada de nivel socioeconómico en base a variables como educación de los padres, ocupación e ingreso)

-   **mathach**, logro en matemática (_math achievement_)

---
## Práctica: High School & Beyond (HSB) data

-   Level 2 variables:

-   size (matricula)

-   sector (1 = Catholic, 0 = public)

-   pracad (proportion of students in the academic track)

-   disclim (a scale measuring disciplinary climate)

-   himnty (1 = more than 40% minority enrollment, 0 = less than 40%)

-   meanses (mean of the SES values for the students in this school who are included in the level-1 file)

-  **Cluster variable**= id (school id)

---
class: inverse, right, middle

# **ESTA CLASE**

## Datos jerárquicos (= distintos niveles)

## Datos nivel 2 agregados

## Descomposición de la varianza

---
## Librerías y datos

### Librerías

```r
pacman::p_load(
haven,  # lectura de datos formato externo
car, # varias funciones, ej scatterplot
dplyr, # varios gestión de datos
stargazer, # tablas
corrplot, # correlaciones
ggplot2, # gráficos
lme4) # multilevel
```

### Datos
.medium[

```r
mlm <-read_dta("http://www.stata-press.com/data/mlmus3/hsb.dta")
```
]

---
## Ajuste datos

.medium[

```r
dim(mlm)
```

```
## [1] 7185   26
```

```r
names(mlm)
```

```
##  [1] "minority" "female"   "ses"      "mathach"  "size"     "sector"  
##  [7] "pracad"   "disclim"  "himinty"  "schoolid" "mean"     "sd"      
## [13] "sdalt"    "junk"     "sdalt2"   "num"      "se"       "sealt"   
## [19] "sealt2"   "t2"       "t2alt"    "pickone"  "mmses"    "mnses"   
## [25] "xb"       "resid"
```
]

Seleccionar variables de interés
.medium[

```r
mlm=mlm %>% select(minority,female,ses,mathach,size,
  sector,mnses,schoolid) %>% as.data.frame()
```
]

---
## Nota: sobre `%>%`

- `%>%` es conocido como "pipe operator", operador pipa o simplemente pipa

- proviene de la librería `magrittr`, que es utilizada en `dplyr`

- objetivo: hacer más fácil y eficiente el código, incorporando varias funciones en una sola línea / comando

- avanza desde lo más general a lo más específico

---
## Descriptivos generales

.medium[

```r
stargazer(as.data.frame(mlm),
          title = "Descriptivos generales", type='text')
```

```
## 
## Descriptivos generales
## ===================================================================
## Statistic   N     Mean    St. Dev.   Min   Pctl(25) Pctl(75)  Max  
## -------------------------------------------------------------------
## minority  7,185   0.275     0.446     0       0        1       1   
## female    7,185   0.528     0.499     0       0        1       1   
## ses       7,185  0.0001     0.779   -3.758  -0.538   0.602   2.692 
## mathach   7,185  12.748     6.878   -2.832  7.275    18.317  24.993
## size      7,185 1,056.862  604.172   100     565     1,436   2,713 
## sector    7,185   0.493     0.500     0       0        1       1   
## mnses     7,185  0.0001     0.414   -1.194  -0.323   0.327   0.825 
## schoolid  7,185 5,277.898 2,499.578 1,224   3,020    7,342   9,586 
## -------------------------------------------------------------------
```
]

---
## Descriptivos generales

```r
hist(mlm$mathach, xlim = c(0,30))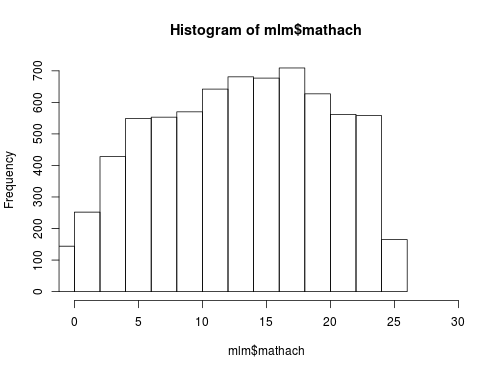
```

![](3jerarquicos_files/figure-html/unnamed-chunk-7-1.png)

---
## Descriptivos generales

```r
scatterplot(mlm$mathach ~ mlm$ses,
  data=mlm, xlab="SES", ylab="Math Score",
  main="Math on SES", smooth=FALSE)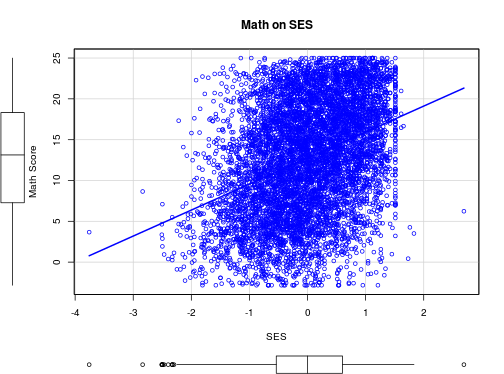
```

![](3jerarquicos_files/figure-html/unnamed-chunk-8-1.png)

---
## Descriptivos generales

```r
cormat=mlm %>%
  select(mathach,ses,sector,size, mnses) %>%
  cor()

round(cormat, digits=2)
```

```
##         mathach   ses sector  size mnses
## mathach    1.00  0.36   0.20 -0.05  0.34
## ses        0.36  1.00   0.19 -0.07  0.53
## sector     0.20  0.19   1.00 -0.42  0.36
## size      -0.05 -0.07  -0.42  1.00 -0.13
## mnses      0.34  0.53   0.36 -0.13  1.00
```

---
## Descriptivos generales

```r
corrplot.mixed(cormat)
```

![](3jerarquicos_files/figure-html/unnamed-chunk-10-1.png)

---
## Datos agregados

- Datos nivel 2:
  - propios/idiosincráticos (ej: tamaño)
  - agregados: generados a partir de datos nivel 1

--
- Una de las particularidades de los métodos multinivel es que permiten estimar y comparar efectos de la misma variable individual y agregada

- Ejemplo:
  - nivel socioeconómico individual
  - nivel socioeconómico de la escuela

- Para ello, se procede a "agregar", generando una base de datos a nivel 2

---
## Datos agregados

- Usando la funcion `group_by` (agrupar por) de la librería `dplyr`
- Se agrupa por la variable **cluster**, que identifica a las unidades de nivel 2 (en este caso, `schoolid`)
- Por defecto se hace con el promedio, pero se pueden hacer otras funciones como contar, porcentajes, mediana, etc.

```r
agg_mlm=mlm %>% group_by(schoolid) %>%
  summarise_all(funs(mean)) %>% as.data.frame()
```

--
Entonces,
  - generamos el objeto `agg_mlm` desde el objeto `mlm`
  - agrupando por la variable cluster `schoolid`
  - agregamos (colapsamos) todas `summarise_all` por el promedio `funs(mean)`

---
## Datos agregados

### Descriptivos

.medium[

```r
stargazer(agg_mlm, type = "text")
```

```
## 
## =================================================================
## Statistic  N    Mean    St. Dev.   Min   Pctl(25) Pctl(75)  Max  
## -----------------------------------------------------------------
## schoolid  160 5,309.994 2,547.683 1,224  3,018.2  7,431.8  9,586 
## minority  160   0.275     0.301   0.000   0.037    0.404   1.000 
## female    160   0.519     0.256   0.000   0.437    0.605   1.000 
## ses       160  -0.006     0.414   -1.194  -0.307   0.314   0.825 
## mathach   160  12.621     3.118   4.240   10.474   14.648  19.719
## size      160 1,097.825  629.506   100    588.5    1,526   2,713 
## sector    160   0.438     0.498     0       0        1       1   
## mnses     160  -0.006     0.414   -1.194  -0.307   0.314   0.825 
## -----------------------------------------------------------------
```
]

---
## Comparación Modelos

- Modelo con datos individuales

```r
reg<- lm(mathach~ses+female+sector, data=mlm)
```

- Modelo con datos agregados

```r
reg_agg<- lm(mathach~ses+female+sector, data=agg_mlm)
```

- Generación tabla

```r
stargazer(reg,reg_agg,
  column.labels=c("Individual","Agregado"),
  type ='text')
```

---
## Comparación Modelos

.small[

```
## 
## ======================================================================
## Dependent variable: 
## --------------------------------------------------
## mathach 
## Individual Agregado 
## (1) (2) 
## ----------------------------------------------------------------------
## ses 2.884*** 5.192*** 
## (0.097) (0.372) 
## 
## female -1.404*** -1.971*** 
## (0.149) (0.562) 
## 
## sector 1.963*** 1.253*** 
## (0.152) (0.306) 
## 
## Constant 12.521*** 13.128*** 
## (0.131) (0.348) 
## 
## ----------------------------------------------------------------------
## Observations 7,185 160 
## R2 0.160 0.675 
## Adjusted R2 0.159 0.668 
## Residual Std. Error 6.307 (df = 7181) 1.796 (df = 156) 
## F Statistic 454.392*** (df = 3; 7181) 107.779*** (df = 3; 156)
## ======================================================================
## Note: *p<0.1; **p<0.05; ***p<0.01
```
]

---
class: roja, middle, center

# ¿Qué problema puede haber al estimar un mismo modelo para variables individuales y agregadas?

---
## Implicancias estimación individual/agregada

- diferencias entre los coeficientes: riesgo de falacia ecológica / individualista

- diferencias entre los errores estándar, recordar

$$ \sigma_{est} = \sqrt{\frac{sum(Y-Y')^{2}}{N}}  $$

---
## Implicancias estimación individual/agregada

![](3jerarquicos_files/figure-html/unnamed-chunk-17-1.png)

---
## Implicancias estimación individual/agregada

- inflación de errores estándar para variables nivel 1 estimadas como agregadas, ej: female agregado (riesgo error tipo II)

- contracción de errores estándar para variables nivel 2 estimadas como individuales, ej: sector individual (error tipo I)

## Solución: 
### Modelo que ajuste errores estándar según el tipo de variable nivel 1 y nivel 2 = MULTINIVEL

---
class: inverse, middle, right

# Descomposición de varianza

---
## Descomposición de la varianza

### Idea base de modelos multinivel: la varianza de la variable dependiente se puede descomponer en distintos niveles

- Estas varianzas son:

- varianza Nivel 1: dentro o "within", en relación al promedio individual

- varianza Nivel 2: entre o "between", en relación al promedio de los grupos
  
  - varianza Nivel `$j$` ...

---
## Varianzas

.medium[

```r
 ggplot(merged, 
        aes(x=mathach, colour=id_data)) + 
        geom_density() + theme(text = element_text(size = 20))
```

![](3jerarquicos_files/figure-html/unnamed-chunk-18-1.png)
]

---
# Descomposición de la varianza

![](images/withinbetween.jpg)

---
# Descomposición de la varianza

.center[
![](images/withinbetween2.png)
]

`$$var_{tot}=var_{dentro}+var_{entre}$$`

---
class: middle

.pull-left[
![](images/pie.png)

]

.pull-right[
 
# ¿Qué proporción de la varianza es "entre" unidades de nivel 2?
 ]

---
## Varianzas

```r
var_tot = var (mlm$mathach)
var_entre= var (agg_mlm$mathach)
```

Proporción de varianza _entre_ (estimación "bruta"):

```r
var_tot
```

```
## [1] 47.31026
```

```r
var_entre
```

```
## [1] 9.71975
```

```r
var_entre/var_tot
```

```
## [1] 0.205447
```

---
# Varianzas

![](images/var_pred.png)

---
class: roja, middle, center

# Correlación intra-clase

## "Proporción de la varianza de la variable dependiente que se asocia a la pertenencia a unidades de nivel 2"

---
class: right

# Correlación intra-clase

### - Expresa de manera simple la descomposición de la varianza

### - Informa la relevancia de el uso de modelos multinivel

### - Anticipa el posible efecto de predictores de nivel 2 (poca varianza, poco que explicar)

---
class: inverse

# RESUMEN

- Errores de estimación al incluir predictores de nivel 2 en regresión de un nivel (OLS)

- Modelo multinivel: ajusta los efectos y errores según el nivel del predictor

- Descomposición de la varianza:

- permite obtener la proporción de la variable dependiente que se asocia a la pertenencia a unidades de nivel 2 (correlación intra-clase)
  
  - base de modelo multinivel: cada predictor se ajusta según su nivel a la varianza correspondiente de la dependiente

---
class: inverse, middle, center

# Próxima clase

## Estimación modelo multinivel - librería `lme4` de `R`

---
class: inverse

.pull-left[.center[
 
 
 
 
 
 
 
 
![:scale 70%](https://multinivel.netlify.com/images/hex_eic2.png)]]

.pull-right[
# Modelos Multinivel
### Juan Carlos Castillo
### Sociología FACSO - UChile
### 2do Sem 2019
### [multinivel.netlify.com](https://multinivel.netlify.com)

## Sesión 3: Regresión con datos individuales y agregados
]