class: bottom, right, inverse <!--- Para correr en ATOM - open terminal, abrir R (simplemente, R y enter) - rmarkdown::render('static/docpres/02_bases/2mlmbases.Rmd', 'xaringan::moon_reader') About macros.js: permite escalar las imágenes como [scale 50%](path to image), hay si que grabar ese archivo js en el directorio. ---> .pull-left[.center[ <br> <br> <br> <br> <br> <br> <br> <br> ]] .pull-right[ # Modelos Multinivel ### Juan Carlos Castillo ### Sociología FACSO - UChile ### 2do Sem 2019 ### [multinivel.netlify.com](https://multinivel.netlify.com) <br> ## Sesión 4: Correlación intra-clase y efectos aleatorios ] --- class: roja, middle, center # Resumen sesión anterior --- ## Parámetros 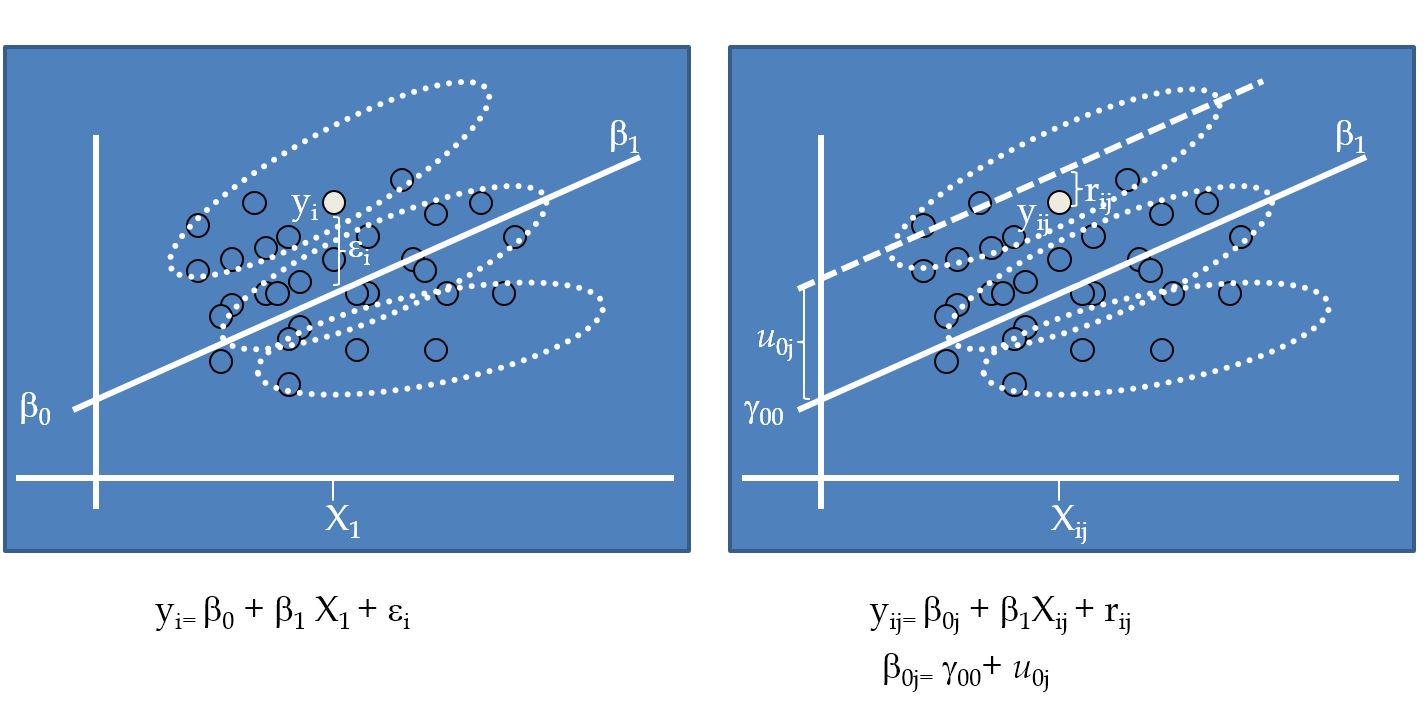 --- ## Comparación Modelos .small[ ``` ## ## ====================================================================== ## Dependent variable: ## -------------------------------------------------- ## mathach ## Individual Agregado ## (1) (2) ## ---------------------------------------------------------------------- ## ses 2.884*** 5.192*** ## (0.097) (0.372) ## ## female -1.404*** -1.971*** ## (0.149) (0.562) ## ## sector 1.963*** 1.253*** ## (0.152) (0.306) ## ## Constant 12.521*** 13.128*** ## (0.131) (0.348) ## ## ---------------------------------------------------------------------- ## Observations 7,185 160 ## R2 0.160 0.675 ## Adjusted R2 0.159 0.668 ## Residual Std. Error 6.307 (df = 7181) 1.796 (df = 156) ## F Statistic 454.392*** (df = 3; 7181) 107.779*** (df = 3; 156) ## ====================================================================== ## Note: *p<0.1; **p<0.05; ***p<0.01 ``` ] --- ## Implicancias estimación individual/agregada - diferencias entre los coeficientes: riesgo de falacia ecológica / individualista - diferencias entre los errores estándar, recordar $$ \sigma_{est} = \sqrt{\frac{sum(Y-Y')^{2}}{N}} $$ - inflación de errores estándar para variables nivel 1 estimadas como agregadas, ej: female agregado (riesgo error tipo II) - contracción de errores estándar para variables nivel 2 estimadas como individuales, ej: sector individual (error tipo I) --- class: middle ## Solución: Modelo que ajuste errores estándar según el tipo de variable nivel 1 y nivel 2 = MULTINIVEL --- ### Idea base de modelos multinivel: la varianza de la variable dependiente se puede descomponer en distintos niveles - Estas varianzas son: - varianza Nivel 1: dentro o "within", en relación al promedio individual - varianza Nivel 2: entre o "between", en relación al promedio de los grupos - varianza Nivel `\(j\)` ... --- # Descomposición de la varianza .center[  ] `$$var_{tot}=var_{dentro}+var_{entre}$$` --- # Varianzas  --- class: roja, middle, center # Correlación intra-clase ## "Proporción de la varianza de la variable dependiente que se asocia a la pertenencia a unidades de nivel 2" --- class: inverse, middle, right # Esta clase: _Estimación modelo multinivel_ ### librería `lme4` de `R` ### Componentes de la varianza ### Efectos fijos y aleatorios --- # Pasos (usuales) en la estimación del modelo 0 Modelo nulo 1. Modelo con variables individuales 2. Modelo con variables contextuales 3. Modelo con variables individuales y contextuales 4. Modelo con pendiente (individual) aleatoria 5. Modelo con variables individuales, contextuales e interacción entre niveles (cross-level interaction) --- ## 0.Modelo nulo 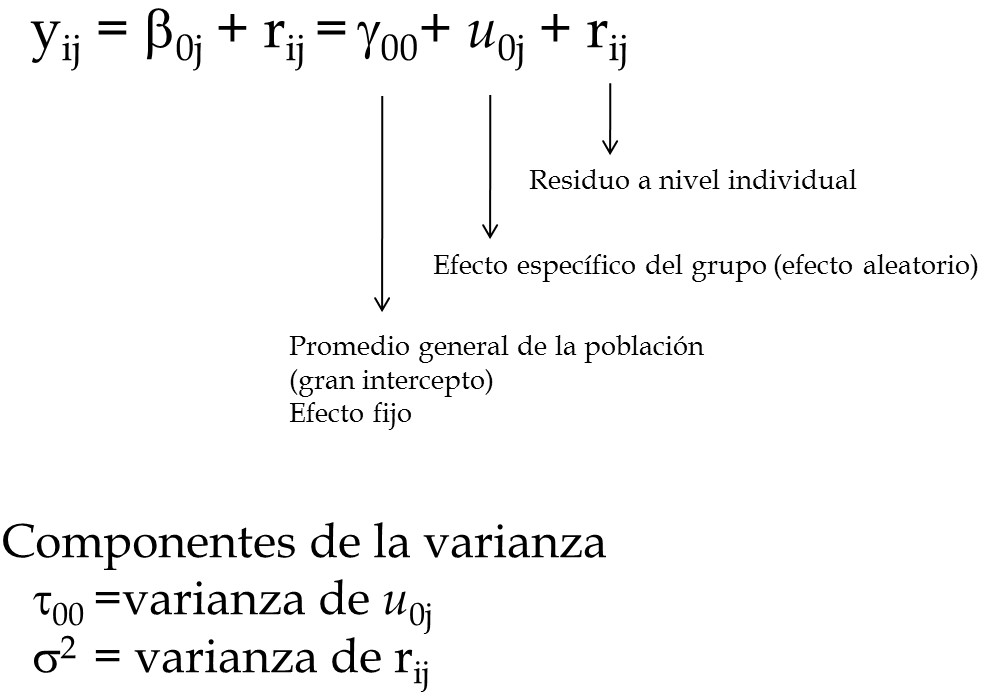 --- ## 1.Modelo con variable independiente individual 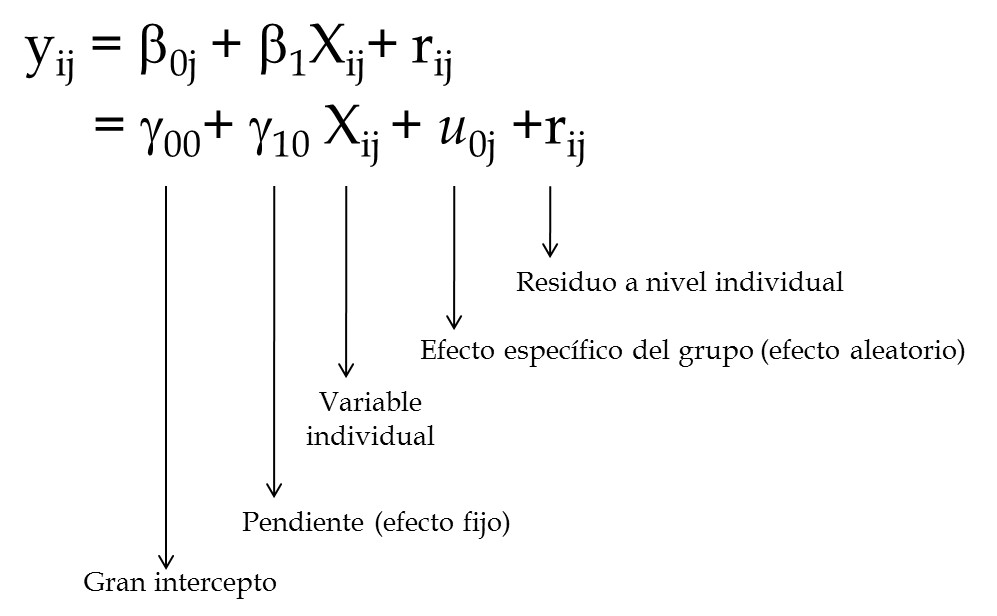 --- ## 2.Modelo con variable independiente grupal 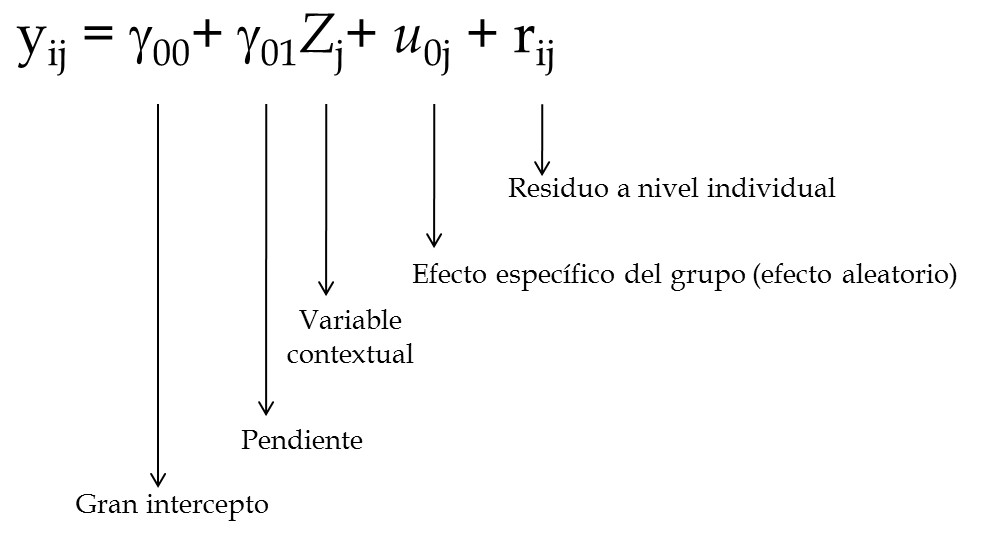 --- ## 3.Modelo con variable independiente individual y grupal  --- ## 4.Modelo con pendiente aleatoria  --- ## 4.Modelo con pendiente aleatoria  --- ## 5.Modelo con interacción entre niveles  "La relación entre X e Y varía entre contextos, y esta variación se asocia a una característica del contexto" *Ej*: la influencia del nivel socioeconómico en rendimiento en lenguaje es moderada por la presencia de bibliotecas en las escuelas --- ## Componentes de la varianza - Los efectos aleatorios asumen una varianza (estimada) en base a una distribución normal - Permiten calcular la correlación intra-clase y distintas medidas de ajuste de los modelos - `\(var \ r_{ij}=\sigma^2\)` (varianza residuos nivel individual) - `\(var \ \mu_{0j}= \tau_{00} = \tau_0^2\)` (varianza asociada a intercepto aleatorio) - `\(var \ \mu_{1j}= \tau_{11} = \tau_1^2\)` (varianza asociada a pendiente aleatoria) - `\(cov (\tau_{00},\tau_{11})= \tau_{01}\)` (covarianza entre intercepto y pendiente) --- ## Componentes de la varianza  --- ## Componentes de la varianza  --- ## ICC - La correlación intra-clase ( `\(\rho\)` ) indica qué porcentaje de la varianza de la variable dependiente se debe a pertenencia a unidades de nivel 2 - Descomposición de la varianza en modelo nulo= `\(Var\ y=\tau_{00} + \sigma^2\)` - Es decir, parte de la varianza se debe a los individuos ( `\(\sigma^2\)` ) y parte al grupo ( `\(\tau_{00}\)` ) - Correlación intra-clase = ICC = `\(\rho=\frac{\tau_{00}}{\tau_{00}+\sigma^2}\)` - Una ICC **baja** indica baja variabilidad de la variable dependiente entre unidades de nivel 2 - _por lo tanto_, menores posibilidades de dar cuenta (*explicar*) de esa varianza con predictores de nivel 2. --- # Ejemplo Estimación en R ### librería lme4 - función lmer (linear mixed effects) - forma general: - `objeto <- lmer (depvar ~ predictor_1 + predictor_2 + predictor_n + (1 | cluster), data=data)` - el objeto contiene la información de la estimación; para ver un resumen, `summary(objeto)`, y de manera más presentable, `screenreg(objeto)` --- # Ejemplo Estimación en R ## -> Práctica B --- class: inverse, bottom .pull-left[.center[ <br> <br> <br> <br> <br> <br> <br> <br> ]] .pull-right[ # Modelos Multinivel ### Juan Carlos Castillo ### Sociología FACSO - UChile ### 2do Sem 2019 ### [multinivel.netlify.com](https://multinivel.netlify.com) ]