class: bottom, right, inverse <!--- Para correr en ATOM - open terminal, abrir R (simplemente, R y enter) - rmarkdown::render('static/docpres/02_bases/2mlmbases.Rmd', 'xaringan::moon_reader') About macros.js: permite escalar las imágenes como [scale 50%](path to image), hay si que grabar ese archivo js en el directorio. ---> .pull-left[.center[ <br> <br> <br> <br> <br> <br> <br> <br> ]] .pull-right[ # Modelos Multinivel ### Juan Carlos Castillo ### Sociología FACSO - UChile ### 2do Sem 2019 ### [multinivel.netlify.com](https://multinivel.netlify.com) <br> ## Sesión 5: Efectos aleatorios ] --- class: roja, middle, center # Resumen sesión anterior ## (... y general) --- ## Parámetros 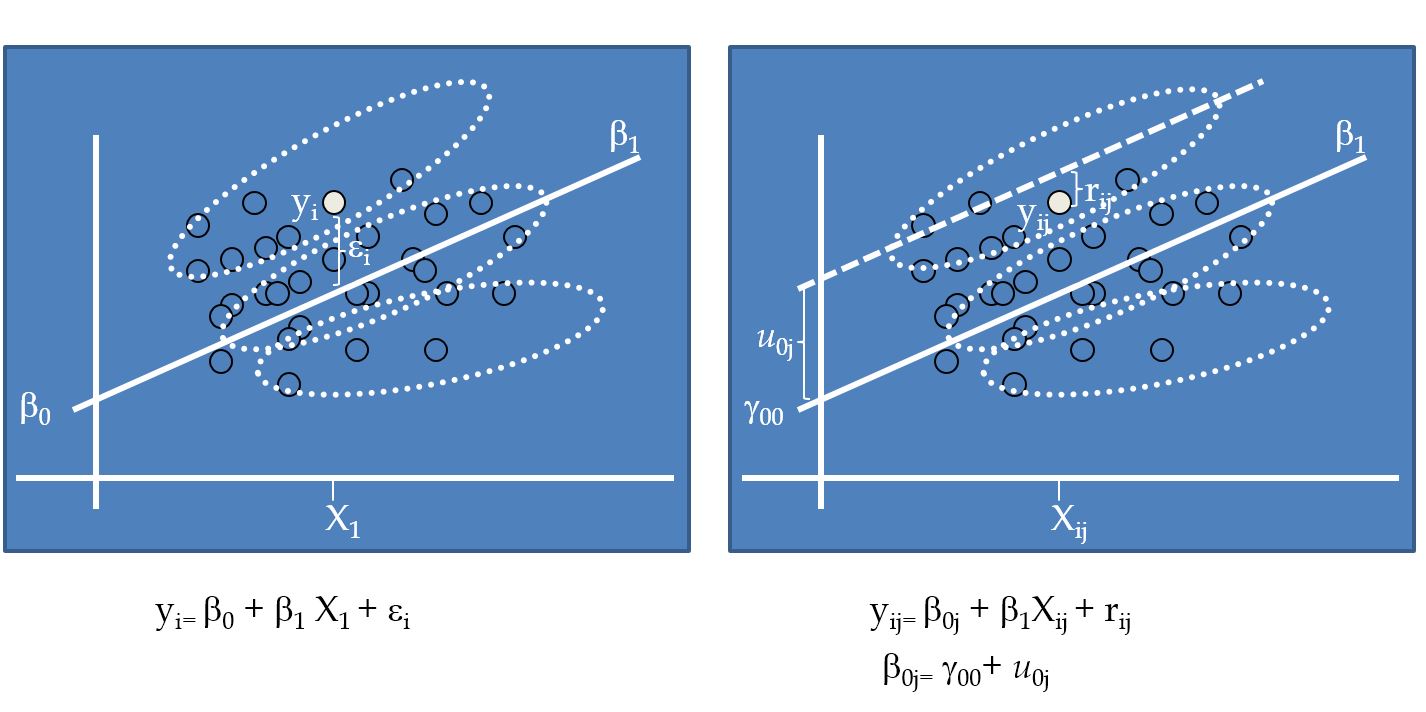 --- ## Comparación Modelos .small[ ``` ## ## ====================================================================== ## Dependent variable: ## -------------------------------------------------- ## mathach ## Individual Agregado ## (1) (2) ## ---------------------------------------------------------------------- ## ses 2.884*** 5.192*** ## (0.097) (0.372) ## ## female -1.404*** -1.971*** ## (0.149) (0.562) ## ## sector 1.963*** 1.253*** ## (0.152) (0.306) ## ## Constant 12.521*** 13.128*** ## (0.131) (0.348) ## ## ---------------------------------------------------------------------- ## Observations 7,185 160 ## R2 0.160 0.675 ## Adjusted R2 0.159 0.668 ## Residual Std. Error 6.307 (df = 7181) 1.796 (df = 156) ## F Statistic 454.392*** (df = 3; 7181) 107.779*** (df = 3; 156) ## ====================================================================== ## Note: *p<0.1; **p<0.05; ***p<0.01 ``` ] --- # Varianzas 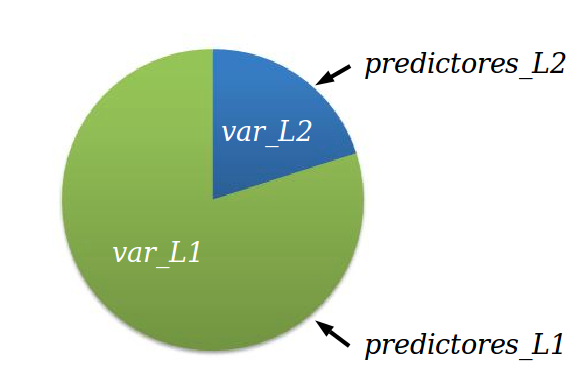 --- class: roja, middle, center # Correlación intra-clase ## "Proporción de la varianza de la variable dependiente que se asocia a la pertenencia a unidades de nivel 2" --- # Pasos (usuales) en la estimación del modelo 0 Modelo nulo 1. Modelo con variables individuales 2. Modelo con variables contextuales 3. Modelo con variables individuales y contextuales 4. Modelo con pendiente (individual) aleatoria 5. Modelo con variables individuales, contextuales e interacción entre niveles (cross-level interaction) --- ## 3.Modelo con variable independiente individual y grupal 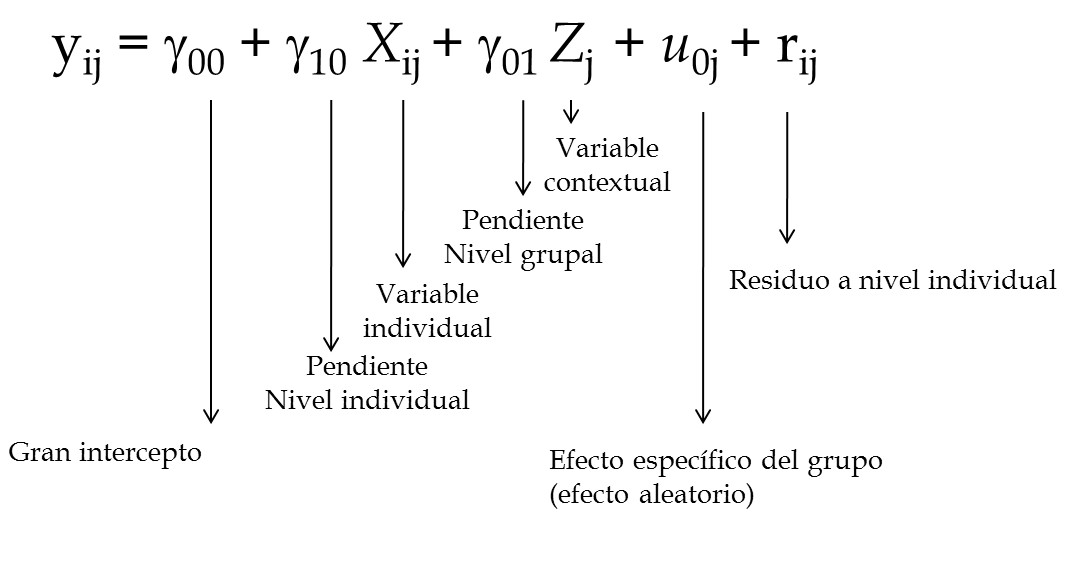 --- ## 4.Modelo con pendiente aleatoria 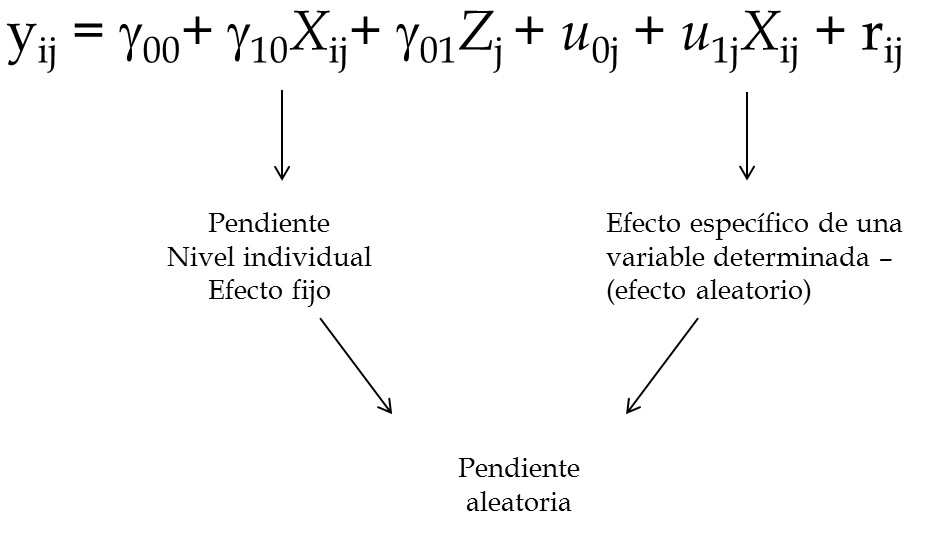 --- ## 4.Modelo con (intercepto y) pendiente aleatoria  --- ## Componentes de la varianza  --- # Ejemplo Estimación en R ### librería lme4 - función lmer (linear mixed effects) - forma general: - `objeto <- lmer (depvar ~ predictor_1 + predictor_2 + predictor_n + (1 | cluster), data=data)` - el objeto contiene la información de la estimación; para ver un resumen, `summary(objeto)`, y de manera más presentable, `screenreg(objeto)` ### -> Práctica B --- class: inverse # Resumen - datos con estructura jerárquica - descomposición de la varianza (de la variable dependiente) según niveles de análisis - correlación intra-clase - variables nivel 1 y nivel 2 (... y nivel _n_) - coeficientes aleatorios (intercepto/pendiente) --- class: roja, middle, center ## Esta sesión: # Profundización efectos aleatorios --- # Modelo con coeficientes aleatorios - El modelo permite la estimación de coeficientes fijos y aleatorios - Fijos: los mismos para todos los casos - Aleatorios: distintos, pero iguales para cada grupo - En general, se utiliza el termino “efectos aleatorios” para el modelo nulo, y coeficientes aleatorios para modelos con pendiente aleatoria. - En este curso, vamos a utilizar “efecto” para referirnos a las desviaciones de cada grupo, y “coeficientes” para la estimación total del grupo (coeficiente=efecto fijo + efecto aleatorio) --- # Modelo con coeficienes aleatorios <br>  --- # Modelo con coeficienes aleatorios - A partir de la estimación del modelo, es posible predecir el valor de los efectos aleatorios ( `\(\mu\)` ) para cada unidad de nivel 2 - Para el intercepto: `\(\mu_{01},\mu_{02},\mu_{03} ... \mu_{0N}\)` - Para la pendiente: `\(\mu_{11},\mu_{12},\mu_{13} ... \mu_{1N}\)` --- ## Notas sobre estimación - 2 tipos de parámetros: fijos y aleatorios (varianzas) - Para poder conocer (estimar) el valor de uno, se requiere el otro, y viceversa - Las varianzas asumen distribución normal - La estimación se efectúa mediante un proceso iterativo, con valores iniciales para los componentes de la varianza, y luego se van ajustando a los datos hasta llegar a la mejor solución --- ## Notas sobre estimación - ¿Cuál es el valor de los componentes de la varianza que maximiza la verosimilitud de encontrar estos valores en la población (distribución normal)? - Los parámetros en multinivel en general se calculan con el método de máxima verosimilitud (**ML**) - Se recomienda la versión restringida (restricted maximum likelihood, **REML**) principalmente en el caso de las muestras pequeñas, produce estimadores menos sesgados para la parte aleatoria (ML es más sesgado hacia la estimación de los componentes de la varianza). --- # (Post) estimación de efectos aleatorios - El valor de los efectos aleatorios se puede (pos)estimar mediante el método de **empirical bayes**, que produce las medias posteriores para cada efecto por unidad de nivel dos (ej:escuela, país) - **Bayesiano** quiere decir que utiliza conocimiento previo (prior) para la estimación, que se relaciona con los parámetros del modelo desde el cual se derivan las medias posteriores - El intercepto por grupo equivale a un promedio ponderado donde se consideran los componentes de la varianza, el N de la unidad 2 y el gran intercepto `\(\gamma_{00}\)` --- ## (Post) estimación de efectos aleatorios - `\(\hat{\beta}^{EB}_{0j}=\gamma_j\hat{\beta}_{0j}+(1-\gamma_j)\hat{\gamma}_{00}\)` - Donde: - `\(\hat{\beta}^{EB}_{0j}\)`: estimador empirical bayes del intercepto para el grupo `\(j\)` - `\(\gamma_j\)` es un ponderador que se define como la confiabilidad del promedio del grupo, y que equivale a `$$\gamma_j=\frac{\tau_{00}}{\tau_{00}+\sigma^2/n_j}$$` - `\(\hat{\beta}_{0j}\)`: es el promedio del grupo - `\(\hat{\gamma}_{00}\)`: gran promedio (efecto fijo intercepto) --- ## (Post) estimación de efectos aleatorios - En esta estimación subyace la idea del **“shrinkage”** (reducción) - Los coeficientes de regresión OLS de cada grupo son reducidos en la dirección del coeficiente promedio para todos los grupos - El grado de “reducción” depende del tamaño del grupo y de la distancia entre el promedio del grupo y el promedio general, es decir, de la *confiabilidad* del promedio del grupo - **Grupos más pequeños y que distan más del promedio serán reducidos de mayor manera hacia el promedio del grupo** --- ## Ej.Estimación de intercepto aleatorio (medias posteriores) .small[ ```r library(lme4) mlm = read_dta("http://www.stata-press.com/data/mlmus3/hsb.dta") results_3 = lmer(mathach ~ 1 + ses + female + mnses + sector + (1 | schoolid), data=mlm) coef(results_3) # coef: comando que muestra coeficientes por grupo $id ``` ``` ## $schoolid ## (Intercept) ses female mnses sector ## 1224 12.707923 2.152109 -1.196833 3.067472 1.251059 ## 1288 13.133888 2.152109 -1.196833 3.067472 1.251059 ## 1296 11.184956 2.152109 -1.196833 3.067472 1.251059 ## 1308 12.475802 2.152109 -1.196833 3.067472 1.251059 ## 1317 11.694382 2.152109 -1.196833 3.067472 1.251059 ## 1358 12.108733 2.152109 -1.196833 3.067472 1.251059 ## 1374 11.257433 2.152109 -1.196833 3.067472 1.251059 ## 1433 14.091378 2.152109 -1.196833 3.067472 1.251059 ## 1436 13.885307 2.152109 -1.196833 3.067472 1.251059 ## 1461 13.567230 2.152109 -1.196833 3.067472 1.251059 ## 1462 12.739162 2.152109 -1.196833 3.067472 1.251059 ## 1477 12.697167 2.152109 -1.196833 3.067472 1.251059 ## 1499 11.302319 2.152109 -1.196833 3.067472 1.251059 ## 1637 11.929833 2.152109 -1.196833 3.067472 1.251059 ## 1906 12.688447 2.152109 -1.196833 3.067472 1.251059 ## 1909 13.273374 2.152109 -1.196833 3.067472 1.251059 ## 1942 14.294538 2.152109 -1.196833 3.067472 1.251059 ## 1946 13.269292 2.152109 -1.196833 3.067472 1.251059 ## 2030 11.372184 2.152109 -1.196833 3.067472 1.251059 ## 2208 12.664836 2.152109 -1.196833 3.067472 1.251059 ## 2277 13.115381 2.152109 -1.196833 3.067472 1.251059 ## 2305 14.031712 2.152109 -1.196833 3.067472 1.251059 ## 2336 14.230611 2.152109 -1.196833 3.067472 1.251059 ## 2458 12.742226 2.152109 -1.196833 3.067472 1.251059 ## 2467 12.534944 2.152109 -1.196833 3.067472 1.251059 ## 2526 14.703184 2.152109 -1.196833 3.067472 1.251059 ## 2626 13.817248 2.152109 -1.196833 3.067472 1.251059 ## 2629 13.997802 2.152109 -1.196833 3.067472 1.251059 ## 2639 12.451456 2.152109 -1.196833 3.067472 1.251059 ## 2651 11.741216 2.152109 -1.196833 3.067472 1.251059 ## 2655 15.735301 2.152109 -1.196833 3.067472 1.251059 ## 2658 11.171818 2.152109 -1.196833 3.067472 1.251059 ## 2755 12.434801 2.152109 -1.196833 3.067472 1.251059 ## 2768 12.147697 2.152109 -1.196833 3.067472 1.251059 ## 2771 13.872969 2.152109 -1.196833 3.067472 1.251059 ## 2818 13.587599 2.152109 -1.196833 3.067472 1.251059 ## 2917 12.832689 2.152109 -1.196833 3.067472 1.251059 ## 2990 13.506608 2.152109 -1.196833 3.067472 1.251059 ## 2995 11.977510 2.152109 -1.196833 3.067472 1.251059 ## 3013 13.141475 2.152109 -1.196833 3.067472 1.251059 ## 3020 13.034486 2.152109 -1.196833 3.067472 1.251059 ## 3039 13.378465 2.152109 -1.196833 3.067472 1.251059 ## 3088 12.404857 2.152109 -1.196833 3.067472 1.251059 ## 3152 13.438828 2.152109 -1.196833 3.067472 1.251059 ## 3332 12.121618 2.152109 -1.196833 3.067472 1.251059 ## 3351 11.012839 2.152109 -1.196833 3.067472 1.251059 ## 3377 12.745610 2.152109 -1.196833 3.067472 1.251059 ## 3427 16.390762 2.152109 -1.196833 3.067472 1.251059 ## 3498 12.361494 2.152109 -1.196833 3.067472 1.251059 ## 3499 11.171742 2.152109 -1.196833 3.067472 1.251059 ## 3533 11.150342 2.152109 -1.196833 3.067472 1.251059 ## 3610 13.749518 2.152109 -1.196833 3.067472 1.251059 ## 3657 13.376831 2.152109 -1.196833 3.067472 1.251059 ## 3688 12.560126 2.152109 -1.196833 3.067472 1.251059 ## 3705 9.645341 2.152109 -1.196833 3.067472 1.251059 ## 3716 13.069586 2.152109 -1.196833 3.067472 1.251059 ## 3838 14.158099 2.152109 -1.196833 3.067472 1.251059 ## 3881 12.083343 2.152109 -1.196833 3.067472 1.251059 ## 3967 13.457604 2.152109 -1.196833 3.067472 1.251059 ## 3992 12.151636 2.152109 -1.196833 3.067472 1.251059 ## 3999 12.251872 2.152109 -1.196833 3.067472 1.251059 ## 4042 11.768611 2.152109 -1.196833 3.067472 1.251059 ## 4173 12.295909 2.152109 -1.196833 3.067472 1.251059 ## 4223 13.938627 2.152109 -1.196833 3.067472 1.251059 ## 4253 10.711470 2.152109 -1.196833 3.067472 1.251059 ## 4292 13.856972 2.152109 -1.196833 3.067472 1.251059 ## 4325 13.772931 2.152109 -1.196833 3.067472 1.251059 ## 4350 11.944010 2.152109 -1.196833 3.067472 1.251059 ## 4383 12.041554 2.152109 -1.196833 3.067472 1.251059 ## 4410 13.211432 2.152109 -1.196833 3.067472 1.251059 ## 4420 14.607346 2.152109 -1.196833 3.067472 1.251059 ## 4458 12.185523 2.152109 -1.196833 3.067472 1.251059 ## 4511 13.646765 2.152109 -1.196833 3.067472 1.251059 ## 4523 9.689643 2.152109 -1.196833 3.067472 1.251059 ## 4530 12.250395 2.152109 -1.196833 3.067472 1.251059 ## 4642 14.288264 2.152109 -1.196833 3.067472 1.251059 ## 4868 10.626388 2.152109 -1.196833 3.067472 1.251059 ## 4931 11.705201 2.152109 -1.196833 3.067472 1.251059 ## 5192 11.122172 2.152109 -1.196833 3.067472 1.251059 ## 5404 11.444270 2.152109 -1.196833 3.067472 1.251059 ## 5619 12.561805 2.152109 -1.196833 3.067472 1.251059 ## 5640 14.159767 2.152109 -1.196833 3.067472 1.251059 ## 5650 13.476656 2.152109 -1.196833 3.067472 1.251059 ## 5667 11.203233 2.152109 -1.196833 3.067472 1.251059 ## 5720 13.241622 2.152109 -1.196833 3.067472 1.251059 ## 5761 12.762717 2.152109 -1.196833 3.067472 1.251059 ## 5762 11.712223 2.152109 -1.196833 3.067472 1.251059 ## 5783 12.871770 2.152109 -1.196833 3.067472 1.251059 ## 5815 11.999153 2.152109 -1.196833 3.067472 1.251059 ## 5819 12.032238 2.152109 -1.196833 3.067472 1.251059 ## 5838 13.273634 2.152109 -1.196833 3.067472 1.251059 ## 5937 13.531048 2.152109 -1.196833 3.067472 1.251059 ## 6074 14.600889 2.152109 -1.196833 3.067472 1.251059 ## 6089 14.761866 2.152109 -1.196833 3.067472 1.251059 ## 6144 11.791491 2.152109 -1.196833 3.067472 1.251059 ## 6170 14.779048 2.152109 -1.196833 3.067472 1.251059 ## 6291 13.352288 2.152109 -1.196833 3.067472 1.251059 ## 6366 13.303538 2.152109 -1.196833 3.067472 1.251059 ## 6397 14.051100 2.152109 -1.196833 3.067472 1.251059 ## 6415 13.285636 2.152109 -1.196833 3.067472 1.251059 ## 6443 12.343162 2.152109 -1.196833 3.067472 1.251059 ## 6464 11.849552 2.152109 -1.196833 3.067472 1.251059 ## 6469 13.153112 2.152109 -1.196833 3.067472 1.251059 ## 6484 13.964413 2.152109 -1.196833 3.067472 1.251059 ## 6578 14.192437 2.152109 -1.196833 3.067472 1.251059 ## 6600 12.635478 2.152109 -1.196833 3.067472 1.251059 ## 6808 11.104890 2.152109 -1.196833 3.067472 1.251059 ## 6816 11.964985 2.152109 -1.196833 3.067472 1.251059 ## 6897 13.660358 2.152109 -1.196833 3.067472 1.251059 ## 6990 10.106525 2.152109 -1.196833 3.067472 1.251059 ## 7011 13.137230 2.152109 -1.196833 3.067472 1.251059 ## 7101 12.457267 2.152109 -1.196833 3.067472 1.251059 ## 7172 9.995348 2.152109 -1.196833 3.067472 1.251059 ## 7232 13.465171 2.152109 -1.196833 3.067472 1.251059 ## 7276 12.897951 2.152109 -1.196833 3.067472 1.251059 ## 7332 12.642896 2.152109 -1.196833 3.067472 1.251059 ## 7341 11.720700 2.152109 -1.196833 3.067472 1.251059 ## 7342 12.364160 2.152109 -1.196833 3.067472 1.251059 ## 7345 12.008754 2.152109 -1.196833 3.067472 1.251059 ## 7364 14.068113 2.152109 -1.196833 3.067472 1.251059 ## 7635 13.087198 2.152109 -1.196833 3.067472 1.251059 ## 7688 15.368184 2.152109 -1.196833 3.067472 1.251059 ## 7697 14.072866 2.152109 -1.196833 3.067472 1.251059 ## 7734 13.289875 2.152109 -1.196833 3.067472 1.251059 ## 7890 11.911265 2.152109 -1.196833 3.067472 1.251059 ## 7919 12.903578 2.152109 -1.196833 3.067472 1.251059 ## 8009 10.836287 2.152109 -1.196833 3.067472 1.251059 ## 8150 12.759413 2.152109 -1.196833 3.067472 1.251059 ## 8165 13.368508 2.152109 -1.196833 3.067472 1.251059 ## 8175 13.026372 2.152109 -1.196833 3.067472 1.251059 ## 8188 12.837975 2.152109 -1.196833 3.067472 1.251059 ## 8193 15.002671 2.152109 -1.196833 3.067472 1.251059 ## 8202 12.209222 2.152109 -1.196833 3.067472 1.251059 ## 8357 14.494788 2.152109 -1.196833 3.067472 1.251059 ## 8367 9.266714 2.152109 -1.196833 3.067472 1.251059 ## 8477 13.822098 2.152109 -1.196833 3.067472 1.251059 ## 8531 12.267737 2.152109 -1.196833 3.067472 1.251059 ## 8627 11.333326 2.152109 -1.196833 3.067472 1.251059 ## 8628 15.827569 2.152109 -1.196833 3.067472 1.251059 ## 8707 12.727478 2.152109 -1.196833 3.067472 1.251059 ## 8775 12.075734 2.152109 -1.196833 3.067472 1.251059 ## 8800 11.596298 2.152109 -1.196833 3.067472 1.251059 ## 8854 10.190318 2.152109 -1.196833 3.067472 1.251059 ## 8857 12.245814 2.152109 -1.196833 3.067472 1.251059 ## 8874 13.954819 2.152109 -1.196833 3.067472 1.251059 ## 8946 12.824607 2.152109 -1.196833 3.067472 1.251059 ## 8983 12.966605 2.152109 -1.196833 3.067472 1.251059 ## 9021 11.234016 2.152109 -1.196833 3.067472 1.251059 ## 9104 12.528424 2.152109 -1.196833 3.067472 1.251059 ## 9158 11.719501 2.152109 -1.196833 3.067472 1.251059 ## 9198 14.372418 2.152109 -1.196833 3.067472 1.251059 ## 9225 13.645952 2.152109 -1.196833 3.067472 1.251059 ## 9292 13.343269 2.152109 -1.196833 3.067472 1.251059 ## 9340 13.529763 2.152109 -1.196833 3.067472 1.251059 ## 9347 12.463314 2.152109 -1.196833 3.067472 1.251059 ## 9359 12.310581 2.152109 -1.196833 3.067472 1.251059 ## 9397 10.983298 2.152109 -1.196833 3.067472 1.251059 ## 9508 12.944517 2.152109 -1.196833 3.067472 1.251059 ## 9550 12.021441 2.152109 -1.196833 3.067472 1.251059 ## 9586 11.831361 2.152109 -1.196833 3.067472 1.251059 ## ## attr(,"class") ## [1] "coef.mer" ``` ] --- ## Ej.estimación de pendiente aleatoria (medias posteriores) .small[ ```r results_4 = lmer(mathach ~ 1 + ses + female + mnses + sector + (1 + ses | schoolid), data=mlm) coef(results_4) # coef: comando que muestra coeficientes por grupo $id ``` ``` ## $schoolid ## (Intercept) ses female mnses sector ## 1224 12.718688 2.229928 -1.185924 3.07283 1.429747 ## 1288 13.118254 2.315323 -1.185924 3.07283 1.429747 ## 1296 11.049900 1.893727 -1.185924 3.07283 1.429747 ## 1308 12.338591 2.009420 -1.185924 3.07283 1.429747 ## 1317 11.563797 1.872895 -1.185924 3.07283 1.429747 ## 1358 12.147338 2.404293 -1.185924 3.07283 1.429747 ## 1374 11.261404 2.215734 -1.185924 3.07283 1.429747 ## 1433 13.862506 2.379662 -1.185924 3.07283 1.429747 ## 1436 13.677847 2.315760 -1.185924 3.07283 1.429747 ## 1461 13.372596 2.834185 -1.185924 3.07283 1.429747 ## 1462 12.237417 1.630519 -1.185924 3.07283 1.429747 ## 1477 12.529403 1.938104 -1.185924 3.07283 1.429747 ## 1499 11.454040 2.467499 -1.185924 3.07283 1.429747 ## 1637 12.006810 2.298976 -1.185924 3.07283 1.429747 ## 1906 12.533231 2.120530 -1.185924 3.07283 1.429747 ## 1909 13.240021 2.296086 -1.185924 3.07283 1.429747 ## 1942 14.193660 2.347177 -1.185924 3.07283 1.429747 ## 1946 13.279340 2.399089 -1.185924 3.07283 1.429747 ## 2030 11.377733 1.835520 -1.185924 3.07283 1.429747 ## 2208 12.493501 2.191759 -1.185924 3.07283 1.429747 ## 2277 12.235888 1.186028 -1.185924 3.07283 1.429747 ## 2305 13.404714 1.442942 -1.185924 3.07283 1.429747 ## 2336 14.155767 2.337910 -1.185924 3.07283 1.429747 ## 2458 12.572619 2.304372 -1.185924 3.07283 1.429747 ## 2467 12.553604 2.254845 -1.185924 3.07283 1.429747 ## 2526 14.521539 2.081324 -1.185924 3.07283 1.429747 ## 2626 13.852562 2.481026 -1.185924 3.07283 1.429747 ## 2629 13.734021 1.793893 -1.185924 3.07283 1.429747 ## 2639 12.054817 1.724141 -1.185924 3.07283 1.429747 ## 2651 11.764077 2.400970 -1.185924 3.07283 1.429747 ## 2655 16.035512 2.674553 -1.185924 3.07283 1.429747 ## 2658 11.059088 1.938731 -1.185924 3.07283 1.429747 ## 2755 12.347354 1.858877 -1.185924 3.07283 1.429747 ## 2768 12.174405 2.338538 -1.185924 3.07283 1.429747 ## 2771 13.980828 2.501683 -1.185924 3.07283 1.429747 ## 2818 13.570566 2.370264 -1.185924 3.07283 1.429747 ## 2917 12.573740 1.848210 -1.185924 3.07283 1.429747 ## 2990 13.342024 2.145252 -1.185924 3.07283 1.429747 ## 2995 11.838660 1.850906 -1.185924 3.07283 1.429747 ## 3013 13.160223 2.400036 -1.185924 3.07283 1.429747 ## 3020 12.865964 2.075182 -1.185924 3.07283 1.429747 ## 3039 13.245543 2.325450 -1.185924 3.07283 1.429747 ## 3088 12.332119 2.064017 -1.185924 3.07283 1.429747 ## 3152 13.438322 2.396298 -1.185924 3.07283 1.429747 ## 3332 12.123488 2.011861 -1.185924 3.07283 1.429747 ## 3351 11.006787 2.015229 -1.185924 3.07283 1.429747 ## 3377 12.371916 1.578023 -1.185924 3.07283 1.429747 ## 3427 16.189039 2.113855 -1.185924 3.07283 1.429747 ## 3498 12.338567 1.739255 -1.185924 3.07283 1.429747 ## 3499 11.078267 1.728836 -1.185924 3.07283 1.429747 ## 3533 10.892292 1.721764 -1.185924 3.07283 1.429747 ## 3610 13.588966 2.422726 -1.185924 3.07283 1.429747 ## 3657 13.581872 2.518576 -1.185924 3.07283 1.429747 ## 3688 12.410368 2.046851 -1.185924 3.07283 1.429747 ## 3705 9.515435 1.541705 -1.185924 3.07283 1.429747 ## 3716 13.442287 2.982233 -1.185924 3.07283 1.429747 ## 3838 13.973101 1.999673 -1.185924 3.07283 1.429747 ## 3881 12.057814 2.124468 -1.185924 3.07283 1.429747 ## 3967 13.500676 2.382283 -1.185924 3.07283 1.429747 ## 3992 12.031843 1.832326 -1.185924 3.07283 1.429747 ## 3999 12.322912 2.532469 -1.185924 3.07283 1.429747 ## 4042 11.656947 1.896690 -1.185924 3.07283 1.429747 ## 4173 12.163090 2.273549 -1.185924 3.07283 1.429747 ## 4223 13.798733 2.279179 -1.185924 3.07283 1.429747 ## 4253 10.273404 1.461998 -1.185924 3.07283 1.429747 ## 4292 13.420117 1.637567 -1.185924 3.07283 1.429747 ## 4325 13.792054 2.438777 -1.185924 3.07283 1.429747 ## 4350 11.946850 2.348998 -1.185924 3.07283 1.429747 ## 4383 12.062749 2.365468 -1.185924 3.07283 1.429747 ## 4410 13.191939 2.287018 -1.185924 3.07283 1.429747 ## 4420 14.621465 2.361761 -1.185924 3.07283 1.429747 ## 4458 12.005552 1.980520 -1.185924 3.07283 1.429747 ## 4511 13.402952 1.861434 -1.185924 3.07283 1.429747 ## 4523 9.513791 1.917411 -1.185924 3.07283 1.429747 ## 4530 12.023144 2.042287 -1.185924 3.07283 1.429747 ## 4642 14.268713 2.533765 -1.185924 3.07283 1.429747 ## 4868 10.512227 1.712426 -1.185924 3.07283 1.429747 ## 4931 11.601200 1.753519 -1.185924 3.07283 1.429747 ## 5192 10.930830 1.907021 -1.185924 3.07283 1.429747 ## 5404 11.464347 1.780138 -1.185924 3.07283 1.429747 ## 5619 12.303160 2.646535 -1.185924 3.07283 1.429747 ## 5640 14.231149 2.534929 -1.185924 3.07283 1.429747 ## 5650 13.273346 1.947294 -1.185924 3.07283 1.429747 ## 5667 11.053304 2.163370 -1.185924 3.07283 1.429747 ## 5720 13.088570 2.244200 -1.185924 3.07283 1.429747 ## 5761 12.686967 2.367094 -1.185924 3.07283 1.429747 ## 5762 11.490666 1.948480 -1.185924 3.07283 1.429747 ## 5783 12.848013 2.277046 -1.185924 3.07283 1.429747 ## 5815 12.018246 2.218960 -1.185924 3.07283 1.429747 ## 5819 12.007924 2.047928 -1.185924 3.07283 1.429747 ## 5838 13.232824 2.193121 -1.185924 3.07283 1.429747 ## 5937 13.467194 2.217537 -1.185924 3.07283 1.429747 ## 6074 14.411909 2.140286 -1.185924 3.07283 1.429747 ## 6089 14.726282 2.339448 -1.185924 3.07283 1.429747 ## 6144 11.821378 2.244576 -1.185924 3.07283 1.429747 ## 6170 14.921393 2.646232 -1.185924 3.07283 1.429747 ## 6291 13.439845 2.383177 -1.185924 3.07283 1.429747 ## 6366 13.139159 2.085864 -1.185924 3.07283 1.429747 ## 6397 14.096697 2.412982 -1.185924 3.07283 1.429747 ## 6415 13.358783 2.500028 -1.185924 3.07283 1.429747 ## 6443 12.111530 1.719363 -1.185924 3.07283 1.429747 ## 6464 11.739236 2.018432 -1.185924 3.07283 1.429747 ## 6469 12.987687 2.152797 -1.185924 3.07283 1.429747 ## 6484 13.838982 1.939921 -1.185924 3.07283 1.429747 ## 6578 14.056908 2.231729 -1.185924 3.07283 1.429747 ## 6600 12.719872 2.703482 -1.185924 3.07283 1.429747 ## 6808 11.072415 2.061460 -1.185924 3.07283 1.429747 ## 6816 11.875889 1.859838 -1.185924 3.07283 1.429747 ## 6897 13.583240 2.589229 -1.185924 3.07283 1.429747 ## 6990 9.886787 1.730689 -1.185924 3.07283 1.429747 ## 7011 13.074902 2.533965 -1.185924 3.07283 1.429747 ## 7101 12.390930 2.019152 -1.185924 3.07283 1.429747 ## 7172 9.723452 1.768357 -1.185924 3.07283 1.429747 ## 7232 13.547272 2.656759 -1.185924 3.07283 1.429747 ## 7276 12.911277 2.557707 -1.185924 3.07283 1.429747 ## 7332 12.481961 2.178251 -1.185924 3.07283 1.429747 ## 7341 11.645933 1.950030 -1.185924 3.07283 1.429747 ## 7342 12.109755 1.945832 -1.185924 3.07283 1.429747 ## 7345 12.058370 2.666148 -1.185924 3.07283 1.429747 ## 7364 13.870748 2.074413 -1.185924 3.07283 1.429747 ## 7635 12.921321 2.210800 -1.185924 3.07283 1.429747 ## 7688 15.182217 2.186222 -1.185924 3.07283 1.429747 ## 7697 14.036678 2.461218 -1.185924 3.07283 1.429747 ## 7734 13.579474 2.775843 -1.185924 3.07283 1.429747 ## 7890 11.620794 1.657940 -1.185924 3.07283 1.429747 ## 7919 12.846154 2.366528 -1.185924 3.07283 1.429747 ## 8009 10.782401 1.743695 -1.185924 3.07283 1.429747 ## 8150 12.609378 1.822869 -1.185924 3.07283 1.429747 ## 8165 13.203263 2.178620 -1.185924 3.07283 1.429747 ## 8175 12.963808 2.083656 -1.185924 3.07283 1.429747 ## 8188 12.842029 2.440730 -1.185924 3.07283 1.429747 ## 8193 14.885212 2.355826 -1.185924 3.07283 1.429747 ## 8202 12.206762 2.303005 -1.185924 3.07283 1.429747 ## 8357 14.518478 2.443492 -1.185924 3.07283 1.429747 ## 8367 9.107836 1.608686 -1.185924 3.07283 1.429747 ## 8477 13.929579 2.607668 -1.185924 3.07283 1.429747 ## 8531 12.233119 2.240760 -1.185924 3.07283 1.429747 ## 8627 11.306052 1.965358 -1.185924 3.07283 1.429747 ## 8628 15.640972 2.182031 -1.185924 3.07283 1.429747 ## 8707 12.716847 2.446274 -1.185924 3.07283 1.429747 ## 8775 11.959725 1.924073 -1.185924 3.07283 1.429747 ## 8800 11.521896 2.237809 -1.185924 3.07283 1.429747 ## 8854 10.184219 2.133731 -1.185924 3.07283 1.429747 ## 8857 12.154898 1.879477 -1.185924 3.07283 1.429747 ## 8874 14.087009 2.565375 -1.185924 3.07283 1.429747 ## 8946 12.734504 1.998656 -1.185924 3.07283 1.429747 ## 8983 12.882791 2.009176 -1.185924 3.07283 1.429747 ## 9021 11.164565 1.905033 -1.185924 3.07283 1.429747 ## 9104 12.411019 2.038344 -1.185924 3.07283 1.429747 ## 9158 11.883105 2.536046 -1.185924 3.07283 1.429747 ## 9198 14.173518 2.479962 -1.185924 3.07283 1.429747 ## 9225 13.609250 2.412433 -1.185924 3.07283 1.429747 ## 9292 13.249691 2.094634 -1.185924 3.07283 1.429747 ## 9340 13.549198 2.294651 -1.185924 3.07283 1.429747 ## 9347 12.299050 2.224249 -1.185924 3.07283 1.429747 ## 9359 12.207862 1.649750 -1.185924 3.07283 1.429747 ## 9397 10.960936 1.983996 -1.185924 3.07283 1.429747 ## 9508 12.858864 2.363500 -1.185924 3.07283 1.429747 ## 9550 12.042265 2.373925 -1.185924 3.07283 1.429747 ## 9586 11.750845 1.908395 -1.185924 3.07283 1.429747 ## ## attr(,"class") ## [1] "coef.mer" ``` ] --- ## Plots  --- ## Plots  --- ## Plots  --- # Resumen predicción efectos aleatorios Usos - Pedagógico: para entender el sentido de la estimación con modelos mixtos (efectos fijos y aleatorios) - Diagnóstico: para analizar y visualizar la variación de unidades de nivel dos a nivel de intercepto y pendiente(s) - Informativo: para conocer los resultados de las unidades de nivel 2 y sus variaciones - Contraste de hipótesis de investigación --- class: inverse, bottom .pull-left[.center[ <br> <br> <br> <br> <br> <br> <br> <br> ]] .pull-right[ # Modelos Multinivel ### Juan Carlos Castillo ### Sociología FACSO - UChile ### 2do Sem 2019 ### [multinivel.netlify.com](https://multinivel.netlify.com) ]