class: bottom, right, inverse <!--- Para correr en ATOM - open terminal, abrir R (simplemente, R y enter) - rmarkdown::render('static/docpres/07_interacciones/7interacciones.Rmd', 'xaringan::moon_reader') About macros.js: permite escalar las imágenes como [scale 50%](path to image), hay si que grabar ese archivo js en el directorio. ---> .pull-left[.center[ <br> <br> <br> <br> <br> <br> <br> <br> ]] .pull-right[ # Modelos Multinivel ### Juan Carlos Castillo ### Sociología FACSO - UChile ### 2do Sem 2019 ### [multinivel.netlify.com](https://multinivel.netlify.com) <br> ## Sesión 8: Centrado de variables ] --- class: roja, middle, center # Resumen --- # Modelos multinivel - Dependencia contextual, datos anidados y falacia ecológica - Estimación de modelo de coeficientes aleatorios - Correlación intra-clase - Pendientes aleatorias - Interacción entre niveles - Ajuste --- class: roja, middle, center # Bases: Centrado en regresión simple --- ## Regresión y centrado - El centrado de las variables en regresión simple posee consecuencias en el valor del intercepto - Intercepto: estimación del valor de la variable dependiente cuando los predictores son 0 - La estimación sin centrar en algunos casos puede llevar a algunos problemas en la interpretación de los parámetros del modelo - El centrado se implementa restando una constante del predictor (usualmente el promedio) --- ## Ejemplo centrado regresión simple Datos: puntaje en CI y en una escala de felicidad 1-7 > mydata felicidad ci 1 1 90 2 3 95 3 4 98 4 6 105 lm(formula = felicidad ~ ci) (Intercept) ci -28.5593 0.3305 ¿Qué significa el valor del intercepto? --- ### Ejemplo centrado en regresión simple .center[ 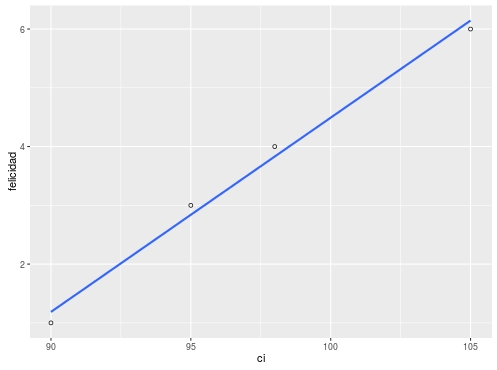 ] --- ### Ejemplo centrado en regresión simple 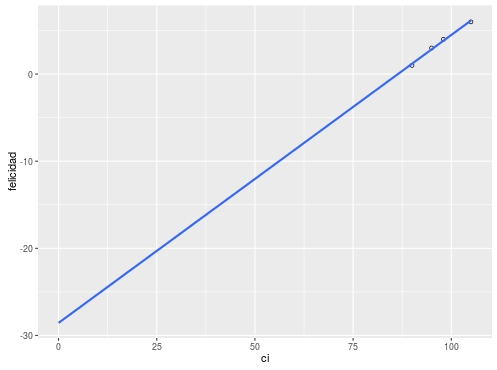 --- ### Ejemplo centrado regresión simple > mydata felicidad ci mean_ci cicent_mean cicent_100 1 1 90 97 -7 -10 2 3 95 97 -2 -5 3 4 98 97 1 -2 4 6 105 97 8 5 lm(formula = felicidad ~ cicent_mean) (Intercept): 3.5000 ; cicent_mean:0.3305 lm(formula = felicidad ~ cicent_100) (Intercept): 4.4915 ; mydata$cicent_100: 0.3305 --- ### Ejemplo centrado en regresión simple 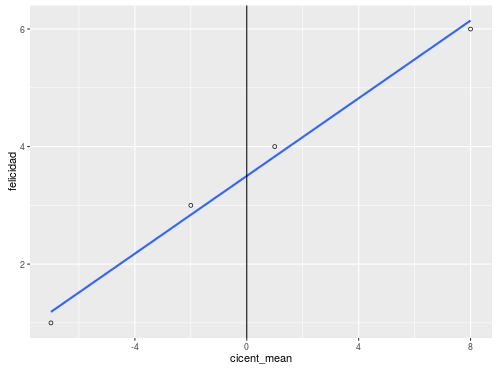 --- ### Ejemplo centrado en regresión simple 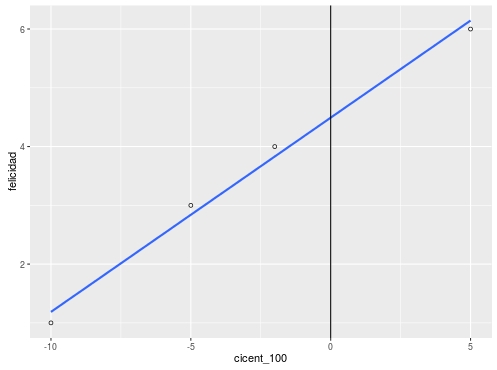 --- ### Ejemplo centrado regresión simple V - `\(\beta\)` constante en todos los modelos, varía solo intercepto - Modelo sin centrar: intercepto -28,5, felicidad para alguien con inteligencia 0 (no tiene mucho sentido ...) - Centrado al promedio: 3.5, estimación de la felicidad para alguien con inteligencia promedio - Centrado a 100: 4.49, estimación de la felicidad para alguien con inteligencia 100 --- class: roja, middle, center # Centrado en modelos multinivel --- # Distintos centrados según nivel - En MLM, las posibilidades de centrado se amplían según la cantidad de niveles que se tengan - Tomando como referencia dos niveles, el centrado de los predictores de nivel uno puede tomar 2 formas principales: - a la gran media o promedio general (**CGM**) - al promedio al interior (within) de grupos/clusters (**CWC**) (nomenclatura Enders & Tofighi, 2007) --- # Distintos centrados según nivel - El **CGM** es equivalente al de regresión simple para el mismo propósito: se resta el valor del promedio general - En el **CWC** se resta el promedio del grupo en lugar de la gran media - A diferencia de regresión simple, las decisiones respecto de centrado afectan más allá del valor del intercepto, influyendo en: - valor de `\(\beta\)` - componentes de la varianza ( `\(\tau_{00},\tau_{11},\tau_{01})\)` - interacciones entre niveles - *CGM y CWC estiman la relación entre X e Y de distinta manera y producen intepretaciones distintas de los parámetros* --- # Distintos centrados según nivel - Pregunta principal: Which form of centering provides interpretable parameter estimates that can be used to address a particular substantive research question? (Enders & Tofighi 2007, p. 122) - Ejemplo: dataset artificial que maximiza las diferencias entre clusters para mostrar mejor los efectos de los distintos tipos de centrado (Enders & Tofighi, 2007) - Variable dependiente: bienestar - Variable independiente nivel 1 ( `\(\gamma_{10}\)` )= horas de trabajo - Variable independiente nivel 2 ( `\(\gamma_{01}\)` )= tamaño del grupo --- ## Centrado a la gran media <br> .center[   ] --- ## CGM - La relación entre las horas de trabajo y bienestar posee componentes a nivel 1 y nivel 2 - Individuos que trabajan más tienen a tener menor bienestar (L1) - Grupos que en promedio trabajan menos poseen menores niveles de bienestar (L2) - Como en regresión simple, en CGM no se altera la estimación de `\(\beta\)`, solo varía la estimación del valor del intercepto ... además de alterar otros parámetros (detalles más adelante) --- ## Comparación con centrado al grupo   --- ## Correlaciones entre especificaciones de centrado .center[  ] --- ## Correlaciones entre especificaciones de centrado En términos de correlación: - La correlación entre variables no varia entre puntajes brutos y centrados CGM - El CWC crea una variable distinta, y por tanto correlaciona distinto con otras - La variable CGM correlaciona tanto con predictores de nivel 1 como de nivel 2 (contiene en su covariación una dimiension *between*) - La variable CWC correlaciona 0 con predictores de nivel 2 (porque su varianza a nivel 2 es 0) --- ## En términos de regresión: .center[  ] --- ## Regresión multinivel y centrado - OLS puede verse como una combinación ponderada de los coeficientes between y within clusters - En CGM, `\(\gamma_{10}\)` es una mezcla de asociación within y between: - “the hierarchical estimator under grand-mean centering is an inappropriate estimator of the person-level [i.e., Level 1] effect. It too is an uninterpretable blend: neither `\(\beta_w\)` nor `\(\beta_b\)`” (Raudenbush and Bryk, 2002, p. 139). --- ## Regresión multinivel y centrado - En CGM, se altera también la estimación de la varianza de las pendientes ( `\(\tau_{11}\)` ) al incorporar elementos between que pueden reducir variabilidad: .center[  ] --- ## En CWC: - No contiene variación entre clusters y por lo tanton o correlaciona con variables de nivel 2 - El intercepto se interpreta como el promedio no ajustado del promedio de los clusters - Por lo tanto, con predictores CWC `\(\gamma_{00}\)` es equivalente al del modelo nulo - En CWC la pendiente corresponde a la regresión within cluster, es un estimador “puro” de la relación nivel 1 entre x e y - La estimación de `\(\tau_{00}\)` con un predictor CWC cuantifica la varianza de los promedios no ajustados; por lo tanto debería ser similar a la de un modelo incondicional (sin predictores) --- ## Centrado y 4 posibles focos de investigación 1. Predictor de nivel 1 2. Predictor de nivel 2 3. Comparar la influencia de un predictor a distintos niveles 4. Efectos de interacción --- ## 1. Predictor de nivel 1 Se recomienda CWC - Estimador “puro” de efectos nivel 1 - Estimación más adecuada de la varianza de la pendiente - Sustantivamente: la posición relativa respecto del grupo es un determinante relevante para los individuos (comportamientos, actitudes, etc.) --- ## 2. Predictor de nivel 2 - Si solo hay predictores de nivel 2, seguir recomendaciones de centrado de OLS - Cuando hay predictores de nivel 1, se recomienda CGM, ya que como contiene varianza between ajusta la estimación de los predictores de nivel 2 - Ej: Enders & Tofighi Tabla 2, ver ajuste de predictor de tamaño (SIZE) cuando HOURS es CGM en lugar de CWC --- class: middle  --- ## 3. Predictor en ambos niveles - Caso de modelos contextuales o composicionales - Requiere usar los puntajes individuales y los promedios de los clusters - Por lo tanto se requiere descomponer la varianza de la pendiente en within y between, - El objetivo es saber si `\(\gamma_{01}\)` es significativo y distinto de `\(\gamma_{10}\)`, es decir, si hay un efecto del grupo más allá del efecto individual - Al estar presentes los promedios de los clusters, `\(\gamma_{10}\)` es equivalente para ambos centrados (CGM=CWC), ya que CGM se encuentra parcializado de los promedios grupales --- - Por lo tanto, dos vías equivalentes para evaluar esto: - CWC: restar ambos coeficientes y ver si la diferencia es significativa - CGM: si `\(\gamma_{01}\)` es significativo implica que la diferencia es significativa  - Para el caso de CWC: `\(\gamma_{10}-\gamma_{01}=-.608-.294=.315\)` - Para CGM: `\(\gamma_{01}=.315\)` (equivalente a la diferencia con CWC), y es significativo. --- ## 4. Interacción entre niveles - La estimación CGM de `\(\gamma_{11}\)` (coeficiente de interacción) es una mezcla poco interpretable de interacciones a ambos niveles - CWC desacopla las interacciones - Por lo tanto, se recomienda CWC en interacciones entre niveles --- class: inverse # Resumen - un predictor nivel 1 no centrado contiene elementos de varianza entre y dentro - por lo tanto, se requiere separar ambas varianzas según las hipótesis a contrastar - en general, para hipótesis de nivel 1 los predictores deben estar centrados al grupo, o controlados por el promedio del predictor por clusters como variable de nivel 2 - de especial relevancia al establecer hipótesis de interacciones entre niveles --- class: inverse, bottom .pull-left[.center[ <br> <br> <br> <br> <br> <br> <br> <br> ]] .pull-right[ # Modelos Multinivel ### Juan Carlos Castillo ### Sociología FACSO - UChile ### 2do Sem 2019 ### [multinivel.netlify.com](https://multinivel.netlify.com) ]